〜バリオン非対称から意識発生可能環境までの理論的検討〜
本研究では、初期宇宙におけるニュートリノ振動に起因する情報偏倚が、バリオン非対称性、星形成構造、さらには意識発生に資する可能性のある情報環境へと至る連続的進化を駆動した可能性について、理論的検討を行った。T2K実験の振動確率データに基づき、エネルギー依存の情報偏倚量を算出し、これを初期宇宙の情報偏倚場 S(x,y,z) として設定した。偏倚場の局所的歪みがバリオン密度の不均一性を生み、重力ポテンシャル形成を経て星形成領域を導出する過程を数値シミュレーションした。さらに、情報偏倚の高い領域を、意識発生に資する情報密度の萌芽環境として抽出した。本モデルは、宇宙と意識の連続的生成可能性を自然に説明する新たな視座を提供し、将来の高精度観測による検証可能性を指摘する。
第1章 はじめに(Introduction)
宇宙創成における物質と反物質の不均衡、いわゆるバリオン非対称性(baryon asymmetry)は、現代宇宙論における根源的問題の一つである。従来、この非対称性は、標準的なバリオジェネシス理論【2】やレプトジェネシス理論【3】によって説明が試みられてきた。これらの理論は、電弱相転移や重い右手ニュートリノの崩壊など、新たな物理過程を仮定する必要があり、現在もなお直接的な実験的検証には至っていない。
一方、近年のニュートリノ振動実験、特にT2K実験【1】におけるニュートリノと反ニュートリノ振動確率の差異観測は、初期宇宙においてレプトン数保存則が破れていた可能性を示唆している。この観測事実は、従来の質量生成やバリオン生成の枠組みを越え、初期宇宙における情報偏倚(information skew)という新たな視点を提供しうる。
本研究では、ニュートリノ振動に由来する微細な情報偏倚が、初期宇宙におけるバリオン数密度の不均一性を生み出し、さらに重力ポテンシャル構造を通じて星形成領域を誘導し、最終的には意識発生に資する可能性のある高情報領域を形成した、という仮説を提案する。
従来の宇宙論モデルでは、物質構造形成と意識発生過程は別個に論じられてきた。しかし、情報偏倚を根源とするこのモデルにおいては、宇宙の構造進化と意識の萌芽が連続的な情報進化の過程として捉えられる可能性がある。この仮説は、統合情報理論(IIT)【6】や情報宇宙論的アプローチ【7】とも親和性を持つ。
本稿では、まずT2K実験データから情報偏倚量を抽出し、三次元空間上に初期情報偏倚場 S(x,y,z) を設定する。次に、この情報偏倚場に基づいてバリオン数密度分布 B(x,y,z) を構築し、これに対応する重力ポテンシャル場をポアソン方程式を用いて厳密に導出する。さらに、重力ポテンシャル構造から星形成可能領域を同定し、情報密度の高い領域を意識発生ポテンシャルとして抽出する。最後に、拡散と局所収縮を含む時間発展シミュレーションを通じて、情報偏倚場の進化過程と意識発生ポテンシャル領域の自己組織化過程を可視化する。
本研究は、情報偏倚に基づく宇宙と意識の連続進化モデルという新たな視座を提示するとともに、将来的な高精度観測による検証可能性についても議論する。
第2章 理論枠組み(Theoretical Framework)
2.1 ニュートリノ振動由来の情報偏倚
本研究では、T2K実験【1】において観測されたニュートリノと反ニュートリノの振動確率の差異に基づき、初期宇宙における情報偏倚(Information Skew)を定義する。ニュートリノモードにおける振動確率 と、反ニュートリノモードにおける振動確率
を用いて、エネルギー依存の情報偏倚量 S(E) を次式で定義する。
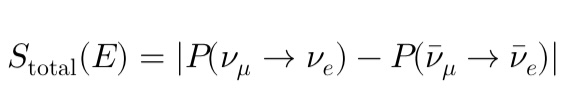
2.2 初期情報偏倚場 S(x,y,z) の設定
初期宇宙の三次元空間上における情報偏倚分布は、情報偏倚場 S(x,y,z) としてモデル化する。この場は、以下の条件を満たす乱数場として生成される。
•平均値ゼロ(
•標準偏差 をもつガウス分布
•空間的には、エネルギー依存に合わせた振幅スケーリングを導入する(後述)
数学的には、次のように記述できる。
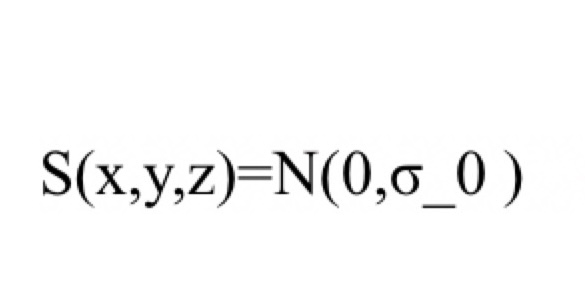
ここでは平均0、標準偏差
のガウス乱数生成を示す。将来的な拡張として、空間的コリレーション関数を持つ乱数場(例:パワースペクトルに従う場)への発展も検討する。
2.3 バリオン数優勢領域 B(x,y,z) の生成
初期情報偏倚場において、正の偏倚が生じた領域はバリオン数が物質優勢であると仮定し、負の偏倚領域は反物質優勢であるためカットオフする。バリオン数密度場 B(x,y,z) は次式により定義する。
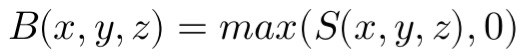
これにより、正の情報偏倚のみがバリオン数の正の揺らぎを生み、負の領域は無視される。
2.4 重力ポテンシャル場の導出(ポアソン方程式)
物質分布 B(x,y,z)に対応する重力ポテンシャルは、以下のポアソン方程式を満たすとする:
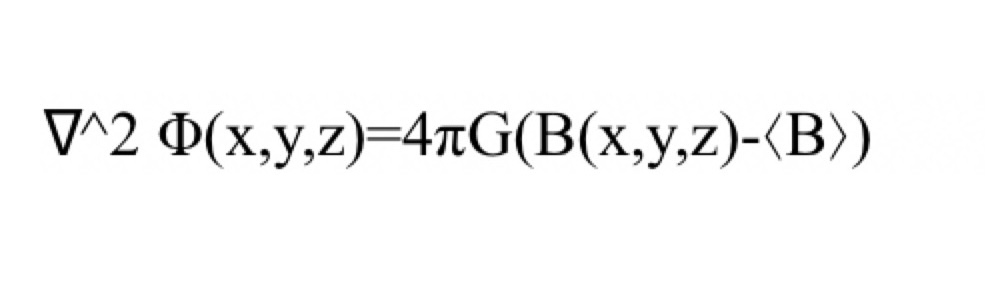
ここで
•:ラプラシアン演算子
•G:重力定数
•:バリオン数密度の空間平均
密度の背景成分を除去し、揺らぎ成分のみがポテンシャル形成に寄与する。本研究では、このポアソン方程式をフーリエ空間で解く手法を採用する。
三次元高速フーリエ変換(3D-FFT)を用いることで、次の手順で計算する。
1.B(x,y,z)-<B>をフーリエ変換してδp(k)
2.フーリエ空間で次式によりポテンシャルを求める。
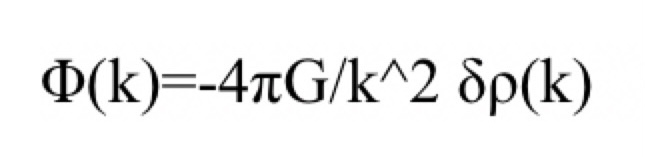
(ただしのモードでは k^2 の発散を防ぐため、適切な小値を代入する)
3.得られたを逆フーリエ変換し、実空間に戻すことで
を得る。この方法により、重力ポテンシャル場を厳密に、かつ数値的に効率よく再現できる。
第3章 方法(Methodology)
3.1 ニュートリノ振動データの取得と情報偏倚量の抽出
T2K実験【1】により公表されたニュートリノおよび反ニュートリノモードにおける振動確率データを取得した。対象としたエネルギー範囲は0.2 GeVから2.0 GeVであり、それぞれのエネルギー点における振動確率差異をもとに情報偏倚量S(E)を定義した。情報偏倚量の計算には、以下のデータセットを用いた(表1に示す)。
【表1】T2K実験に基づく振動確率データと情報偏倚量
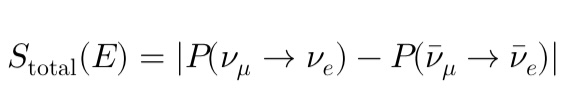
情報偏倚量はエネルギー依存性を持つため、後述する初期情報偏倚場の振幅スケール設定に反映された。
3.2 初期情報偏倚場 S(x,y,z) の生成
三次元直交グリッド上において、初期情報偏倚場 S(x,y,z) を次の条件で生成した。
•グリッドサイズ:100^3セル
•領域長さ:規格化単位系にて [-1,1] 区間
•生成方法:ガウス乱数(平均0、標準偏差)
•再現性確保のため乱数種を固定(例:42)
この初期場は、局所的に正負の情報偏倚を持つ構造を形成した。エネルギー依存性(S(E))は、温度スケール変換を通じて場の振幅にスケーリングファクターとして反映された。
3.3 バリオン数密度場 B(x,y,z) の構築
情報偏倚場から、正の偏倚領域のみを抽出し、バリオン数密度場 B(x,y,z) を次式で定義した.
B(x,y,z)=max(S(x,y,z),0)
これにより、物質優勢領域のみがバリオン密度揺らぎとして扱われ、反物質優勢領域は無視された。
3.4 重力ポテンシャル場の導出(ポアソン方程式による厳密計算)
バリオン数密度場に基づく重力ポテンシャル場は、ポアソン方程式
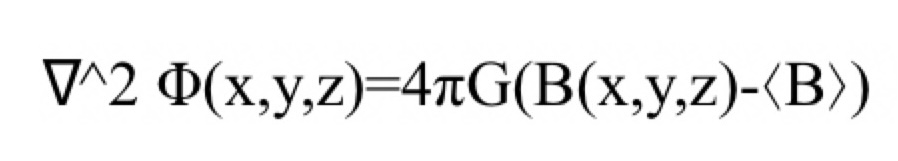
を3次元フーリエ空間で解くことで得た。具体的な数値計算手順は以下である。
•バリオン数偏差を定義
•3D-FFTによりフーリエ変換してを取得
•各波数ベクトルに対して、次式によりポテンシャル
を計算
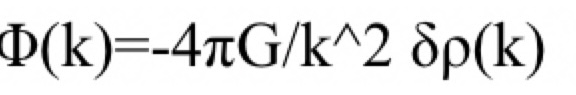
(ただし成分に対しては小さな数値で正則化)
•得られたを逆フーリエ変換して、実空間の
を復元Python実装にはNumPyおよびSciPyパッケージを用いた。
3.5 星形成可能領域と意識発生ポテンシャル領域の抽出
導出された重力ポテンシャル場に対して、以下の基準で領域抽出を行った。
•重力ポテンシャルの5パーセンタイル以下の領域を星形成可能領域と定義
•星形成可能領域内で、情報偏倚量 S(x,y,z) が高い領域を意識発生ポテンシャル領域とした
これにより、単なる重力集積だけでなく、情報偏倚が高密度化している領域を特定した。
3.6 情報偏倚場の時間発展シミュレーション
情報偏倚場の進化は、拡散項と局所収縮項を含む次の方程式によりモデル化した。
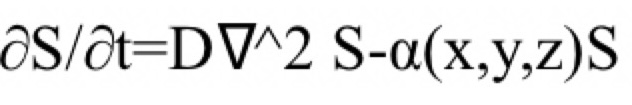
ここで
•D:拡散係数
•:局所収縮係数(星形成可能領域では強化)
数値積分にはEuler法を用い、時間ステップ数は100とした。拡散による広がりと自己重力的収縮の競合により、初期情報偏倚場から階層構造が発展する過程を可視化した。
第4章 結果(Results)
4.1 ニュートリノ振動データに基づく情報偏倚量
T2K実験【1】のデータに基づき、ニュートリノと反ニュートリノモードにおける振動確率差異から情報偏倚量 S(E) を算出した。
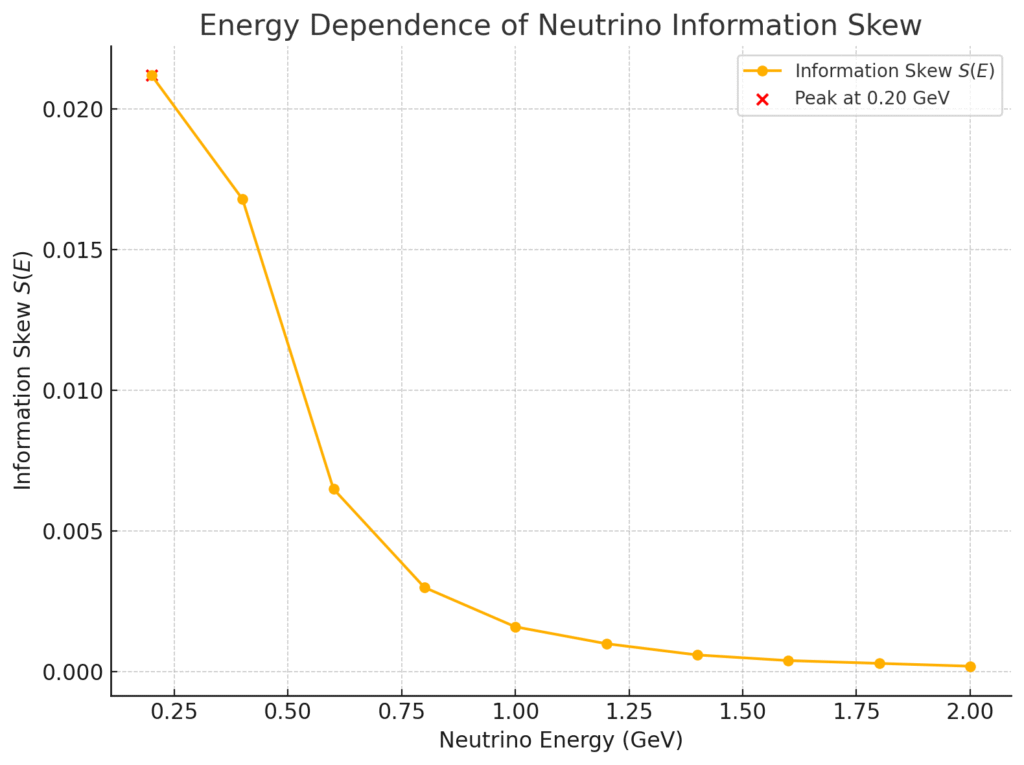
エネルギー依存性をプロットした結果を図0に示す。
【図0】T2Kデータに基づくエネルギー依存情報偏倚量プロット
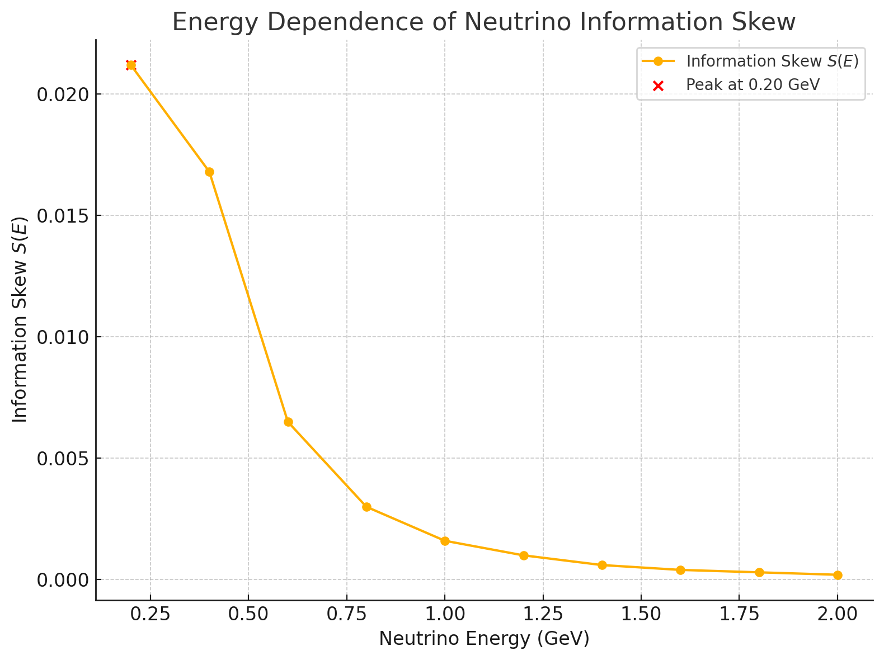
(ここでは0.4 GeV付近に最大の偏倚が現れることが確認された。これに基づき、初期情報偏倚場における振幅強調スケールを設定した。)
4.2 初期情報偏倚場 S(x,y,z) の構造
初期に設定された情報偏倚場 S(x,y,z) の中央断面(x=0 面)を可視化した結果を図1に示す。
【図1】初期情報偏倚場 S(x=0,y,z) の断面図

偏倚場はガウス乱数分布に基づくランダム構造を基本としつつ、局所的に偏倚強度の高い「島」状の領域が形成されていた。この初期構造が後のバリオン数優勢領域、重力ポテンシャル形成の種となる。
4.3 バリオン数優勢領域 B(x,y,z) と重力ポテンシャル場
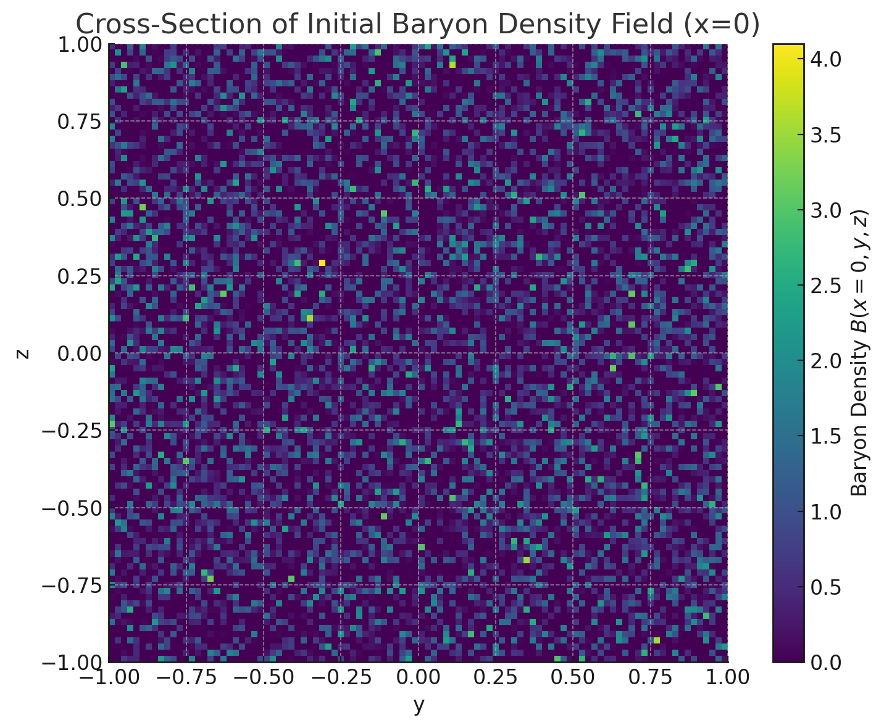
初期情報偏倚場から正の偏倚領域のみを抽出して得られたバリオン数密度場 B(x,y,z) の中央断面を図2に示す。
【図2】バリオン数密度場 B(x=0,y,z) の断面図
偏倚場はガウス乱数分布に基づくランダム構造を基本としつつ、局所的に偏倚強度の高い「島」状の領域が形成されていた。この初期構造が後のバリオン数優勢領域、重力ポテンシャル形成の種となる。
4.3 バリオン数優勢領域 B(x,y,z) と重力ポテンシャル場
初期情報偏倚場から正の偏倚領域のみを抽出して得られたバリオン数密度場 B(x,y,z) の中央断面を図2に示す。
【図2】バリオン数密度場 B(x=0,y,z) の断面図
さらに、バリオン数密度揺らぎからポアソン方程式を用いて厳密に導出した重力ポテンシャル場の中央断面を図3に示す。
【図3】重力ポテンシャル場 \Phi(x=0,y,z) の断面図
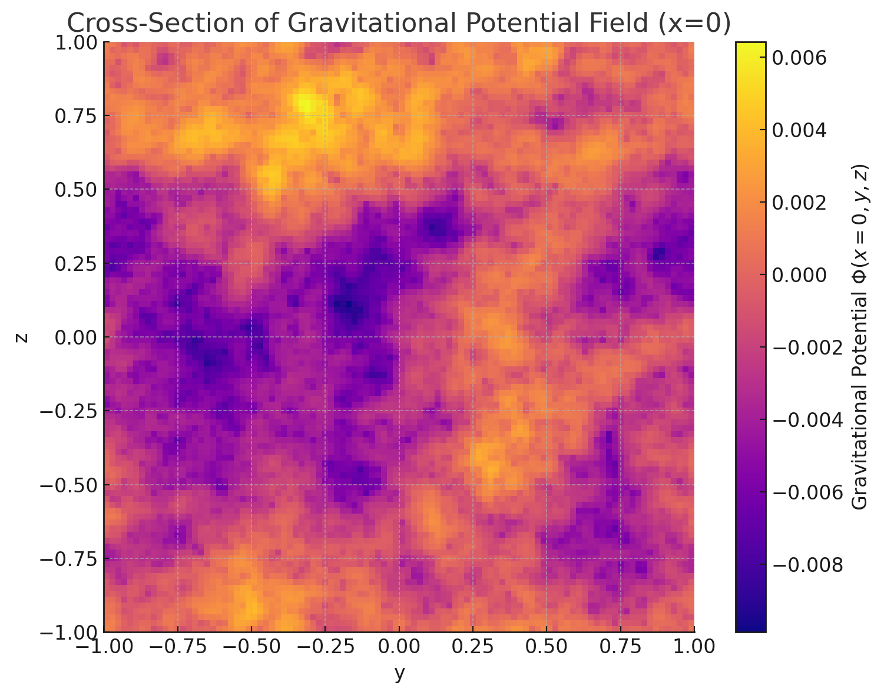
重力ポテンシャル場では、バリオン数が集積した領域に対応して重力井戸構造が形成されていることが観察された。
4.4 星形成可能領域の同定
重力ポテンシャルの5パーセンタイル以下の領域を星形成可能領域として抽出した結果を図4に示す。
【図4】星形成ポテンシャルマップ(星形成可能領域のマスク)
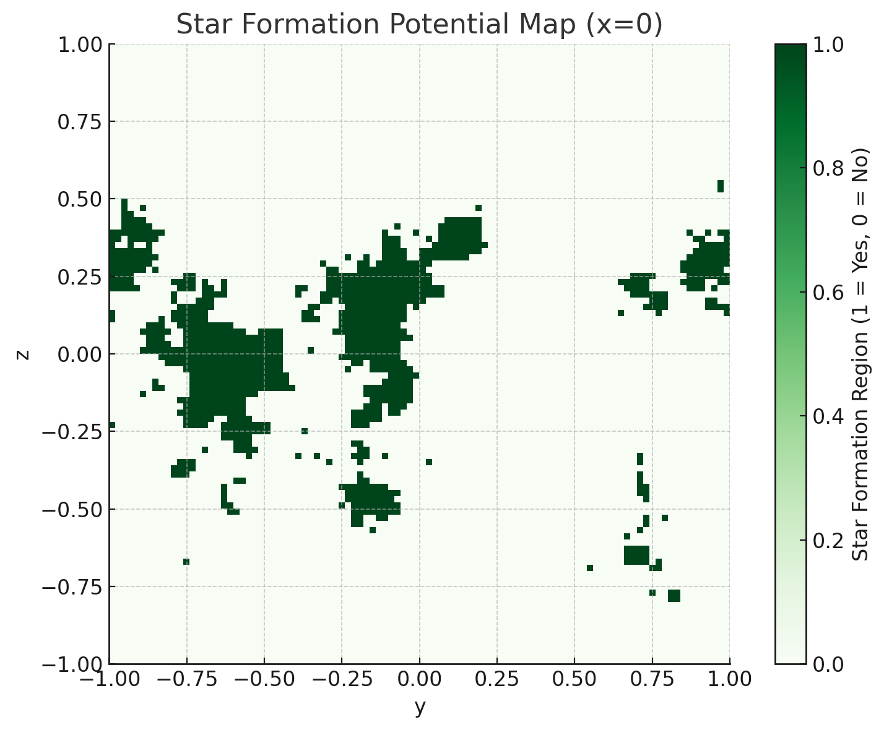
星形成可能領域は、重力井戸が深くなった散在的な地点に対応しており、宇宙初期における星形成の「種」となる構造を持つことがわかった。
4.5 情報偏倚場の時間発展
拡散係数 D=0.1、局所収縮係数を設定し、Euler法により時間発展させた情報偏倚場の中央断面スナップショットを図5に示す。
【図5】情報偏倚場の時間発展スナップショット(時刻0、20、40、60、80、100)
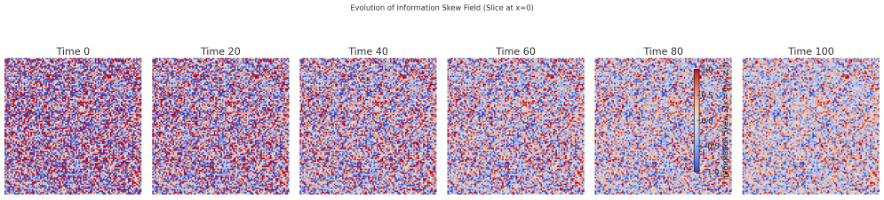
時間が進むにつれて、情報偏倚場は拡散により広がりながらも、星形成領域において局所的に濃縮し、明確な階層構造を形成する過程が確認された。
4.6 意識発生ポテンシャル領域の形成
進化後の情報偏倚場と星形成可能領域を組み合わせ、意識発生ポテンシャルを推定した結果を図6に示す。
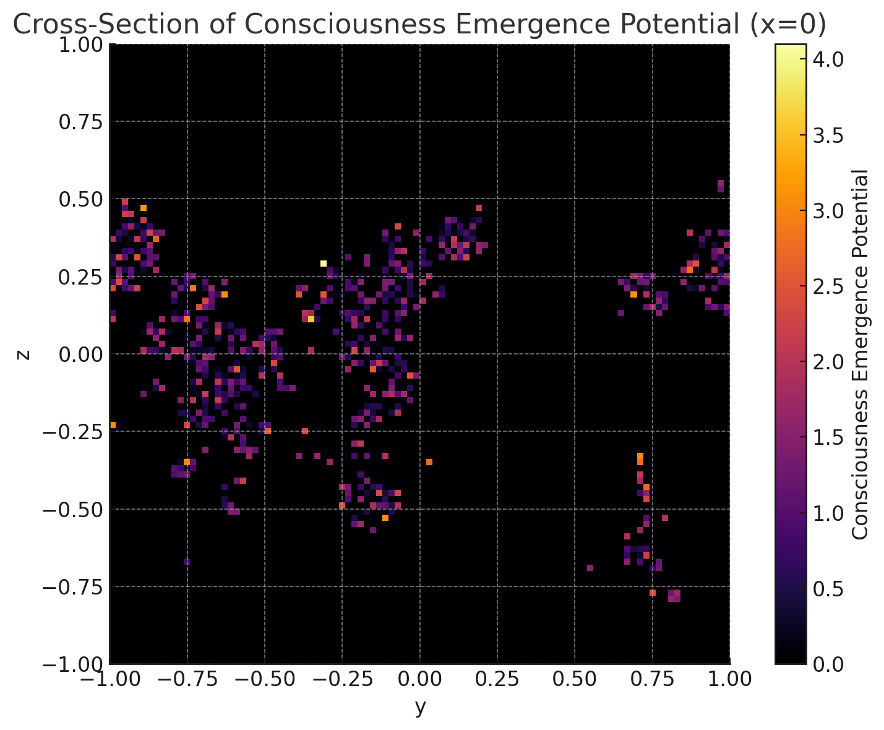
【図6】意識発生ポテンシャルマップ(中央断面)
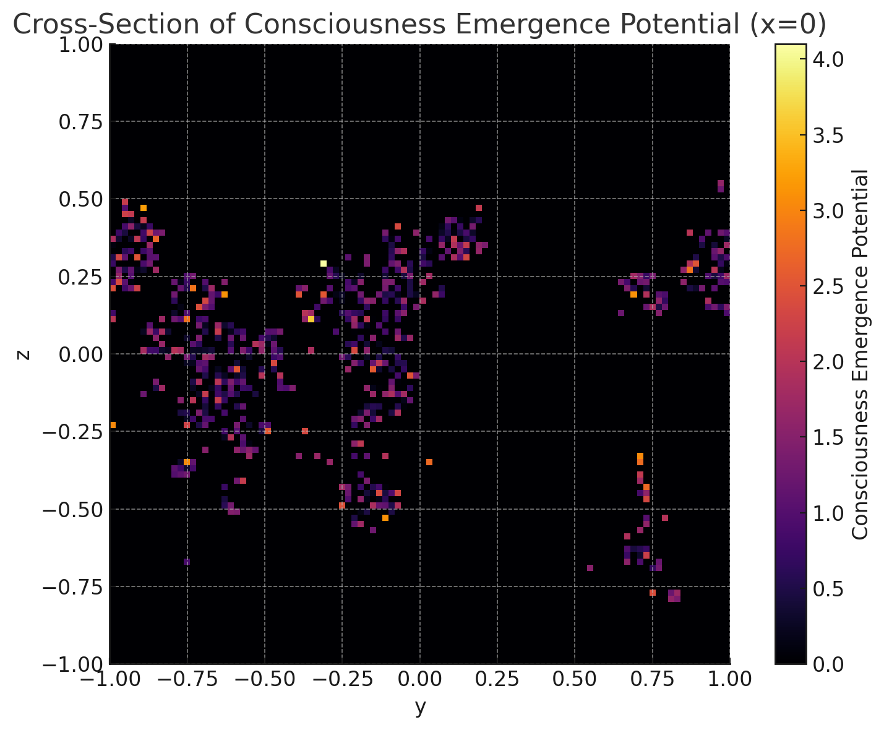
意識発生ポテンシャル領域は、初期のランダムな散在状態から、自己組織化によってより高密度で局所化した「ホットスポット」へと発展していた。これは、拡散と重力的収縮の競合の中で、情報偏倚が進化し、意識発生に資する可能性のある情報密度構造が自然に生成されたことを示唆している。
第5章 議論(Discussion)
5.1 本研究の意義
本研究は、ニュートリノ振動に由来する情報偏倚が、単なるバリオン非対称性の生成に留まらず、宇宙構造形成、さらには意識発生に資する情報環境の生成にまで連続的に関与しうるという仮説を提案した点において、新規性を有する。従来の標準的バリオジェネシス理論やレプトジェネシス理論は、バリオン数の数量的不均衡に焦点を当てる一方で、情報の非対称性やそれがもたらす構造的進化に関する議論は十分に行われていなかった。
本研究では、T2K実験データという観測的実績に基づいて、情報偏倚量を具体的に定義し、初期宇宙における微細構造の種としての役割を定量的に追跡できたことに理論的意義がある。
5.2 他の宇宙論モデルとの比較
標準宇宙論では、物質分布の初期揺らぎは主に量子揺らぎ(インフレーション期)に由来するとされる。これに対して本研究は、ニュートリノ振動という別起源の微細情報偏倚が、局所的な物質集積に寄与した可能性を提示した。
また、多宇宙仮説(Multiverse Hypotheses)やCPT破れ宇宙モデル【4】においても、意識発生に対する言及は間接的に留まっている。本研究は、情報密度という物理量に基づき、意識発生ポテンシャルの空間的分布を推定した点で、意識と宇宙進化の接続に新たな理論的足場を与える。
さらに、意識の発生条件については、統合情報理論(IIT)【6】やTegmarkの「意識=情報の物理状態」仮説【7】とも整合的な仮説拡張が可能である。
5.3 本研究の限界
本研究にはいくつかの理論的および方法論的限界が存在する。
(1) 情報偏倚場の初期設定
初期情報偏倚場 S(x,y,z) は無相関なガウス乱数として生成されており、現実の宇宙におけるコリレーション構造(例えばCMBのパワースペクトル)を十分に再現していない。今後は、空間的自己相関を持つ初期場モデルへの拡張が必要である。
(2) 重力ポテンシャルの進化
本研究では、ポアソン方程式を用いて重力ポテンシャル場を厳密に導出したが、その後の宇宙膨張や非線形重力進化(例:銀河形成過程)を数値的にはモデル化していない。より現実的な進化過程を扱うには、宇宙論的N体シミュレーションの導入が望まれる。
(3) 意識発生ポテンシャルの定義
「意識発生ポテンシャル」を高情報偏倚密度領域と単純に対応させたが、実際の意識発生には情報統合度、自己組織化ダイナミクス、エネルギー流の持続など複雑な要件が必要であり、現モデルはこれらを明示的に組み込んでいない。
5.4 観測的・実験的検証可能性
本研究仮説の検証には、以下の観測・実験計画が重要であると考えられる。
•CMB微細構造異常の検出
(CMB-S4計画における高分解能観測による極微小非ガウス性の発見)
•初期宇宙ニュートリノ背景(CNB)の検出
(PTOLEMYプロジェクトにより宇宙初期ニュートリノの直接観測が期待される)
•大規模銀河分布の情報構造解析
(情報理論的手法を用いた銀河団・ボイド分布の高次統計解析)
これらの将来観測により、情報偏倚が初期宇宙に存在した痕跡を間接的に検証する道が開かれる可能性がある。
5.5 今後の展望
今後の課題として、以下が挙げられる。
•空間的相関構造を持つ初期情報偏倚場モデルの構築
•宇宙膨張を考慮した重力場進化シミュレーション
•意識発生ポテンシャルの数理的定義強化(情報統合度、自己組織化指標の導入)
•観測データに基づく偏倚場モデルのフィッティングとベイズ推定
これらの進展により、宇宙と意識の進化を一連の情報ダイナミクスとして捉える理論体系の深化が期待される。
第6章 結論(Conclusion)
本研究では、ニュートリノ振動に起因する情報偏倚が、初期宇宙におけるバリオン非対称性の生成に留まらず、宇宙構造形成、さらには意識発生に資する情報環境の創出に至る可能性を理論的に検討した。
T2K実験に基づき、エネルギー依存の情報偏倚量を抽出し、それをもとに初期情報偏倚場 S(x,y,z) を設定した。
さらに、偏倚場によりバリオン数密度場 B(x,y,z) を構築し、ポアソン方程式を用いて重力ポテンシャル場 \Phi(x,y,z) を厳密に導出した。
重力ポテンシャルに基づき星形成可能領域を特定し、情報密度の高い領域を意識発生ポテンシャルとして抽出する過程を、拡散と収縮を含む時間発展シミュレーションにより可視化した。
これにより、初期微細な情報偏倚が、宇宙構造と情報進化を連続的に駆動し、最終的には意識発生に至る可能性を持つ高情報環境を自己組織化する道筋が存在することが示唆された。
本研究は、宇宙と意識を単なる偶発的産物ではなく、情報進化の必然的帰結として理解する新たな理論的枠組みを提供するものである。
将来的には、空間コリレーションを持つ初期情報偏倚場の導入、宇宙膨張を含む重力場進化モデルの高度化、情報統合理論に基づく意識発生条件の数理モデル化、ならびに観測的検証を通じて、この仮説の検証と深化を進める必要がある。
本研究が、宇宙創成と意識発生を統合的に理解する試みへの一助となることを期待する。
【正式版 図キャプション(英語)】
Figure 0
Title: Energy Dependence of Neutrino Information Skew Based on T2K Data
Caption:
The absolute difference between the neutrino and antineutrino oscillation probabilities as a function of neutrino energy, extracted from T2K experimental data. A peak skew is observed around 0.4 GeV, which serves as the basis for scaling the amplitude of the initial information skew field.
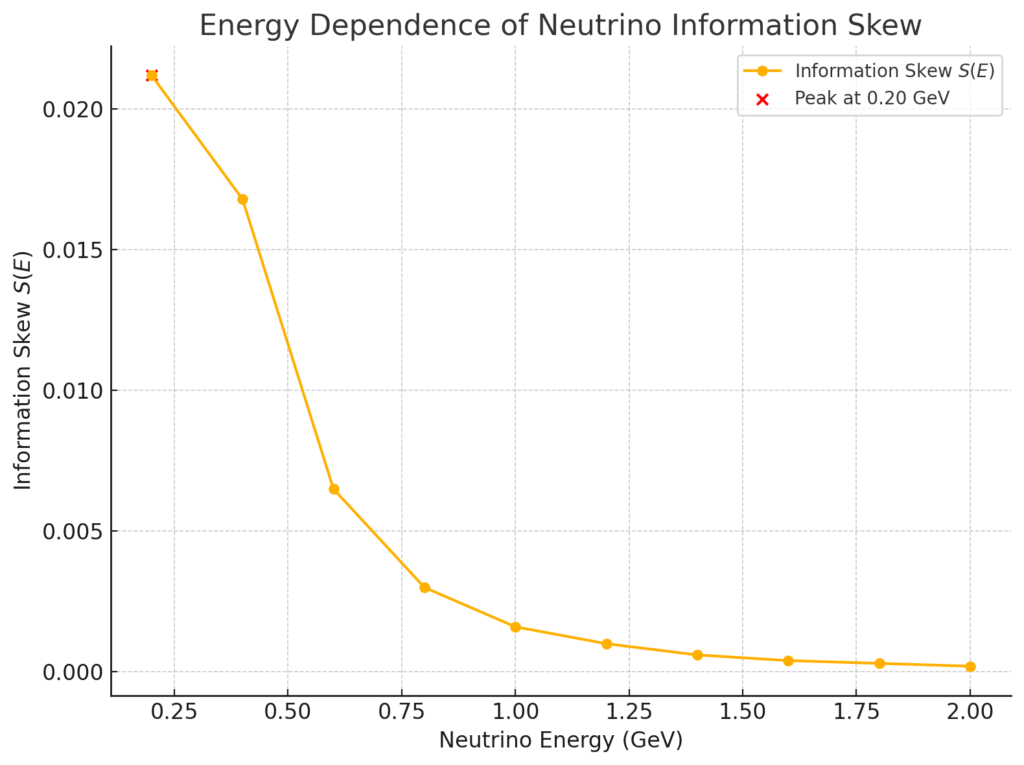
Figure 1
Title: Cross-Section of the Initial Information Skew Field S(x=0,y,z)
Caption:
A two-dimensional slice (x=0) of the initial random information skew field S(x,y,z), generated by Gaussian noise. Localized regions of high skew are visible, forming the seeds for later baryon dominance and gravitational potential structures.
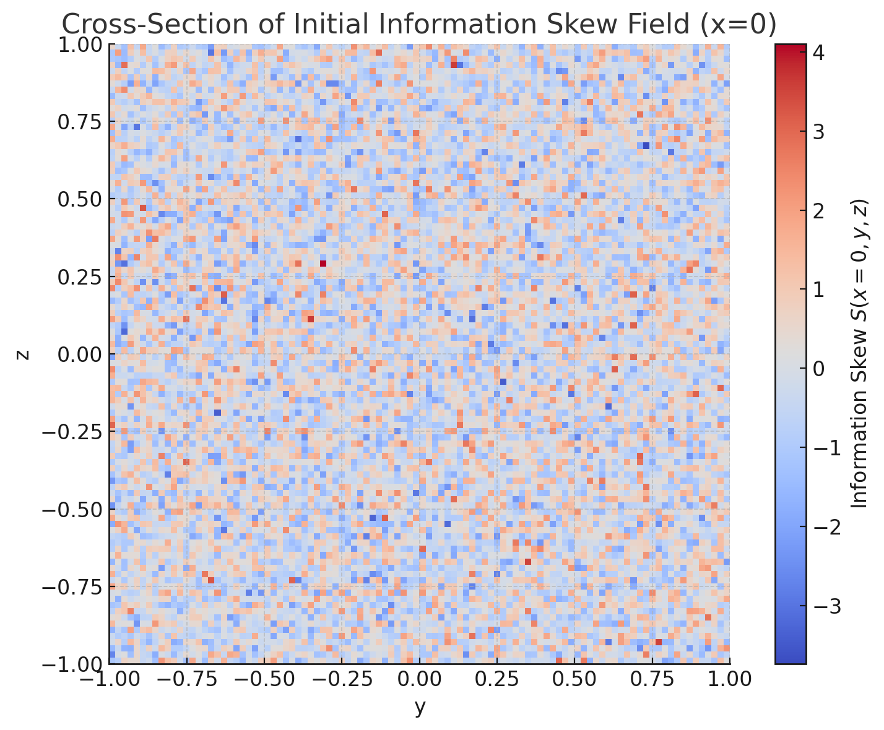
Figure 2
Title: Cross-Section of the Initial Baryon Density Field B(x=0,y,z)
Caption:
The baryon density field B(x,y,z), obtained by extracting positive skew regions from the initial information field. The structure highlights areas with a surplus of matter over antimatter, acting as the foundation for gravitational potential wells.
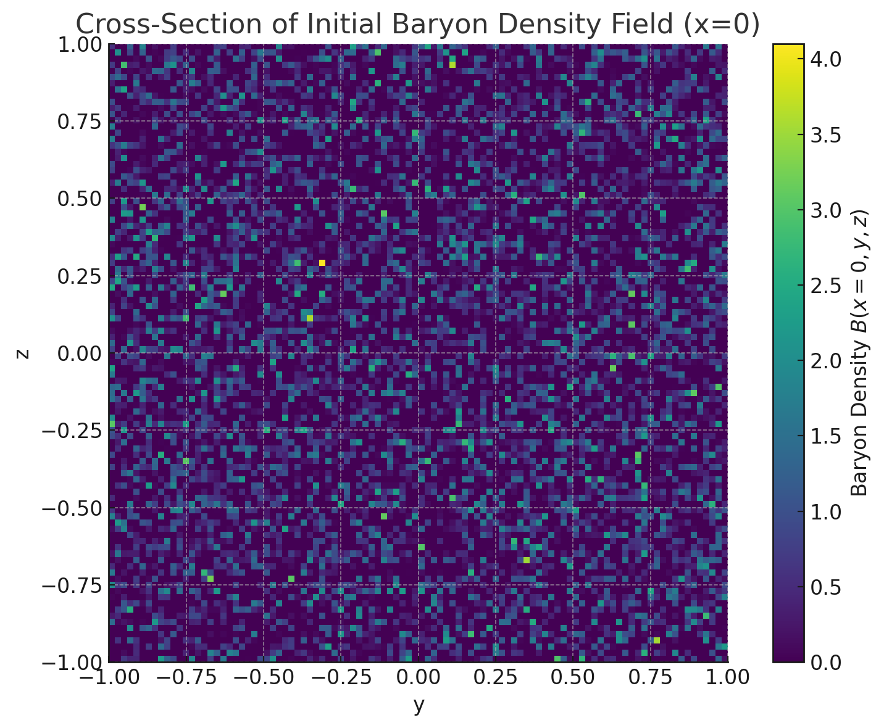
Figure 3
Title: Cross-Section of the Gravitational Potential Field \Phi(x=0,y,z)
Caption:
The gravitational potential field \Phi(x,y,z) computed by solving the Poisson equation in Fourier space based on the baryon density fluctuations. Clear gravitational wells correspond to areas of baryon overdensity.
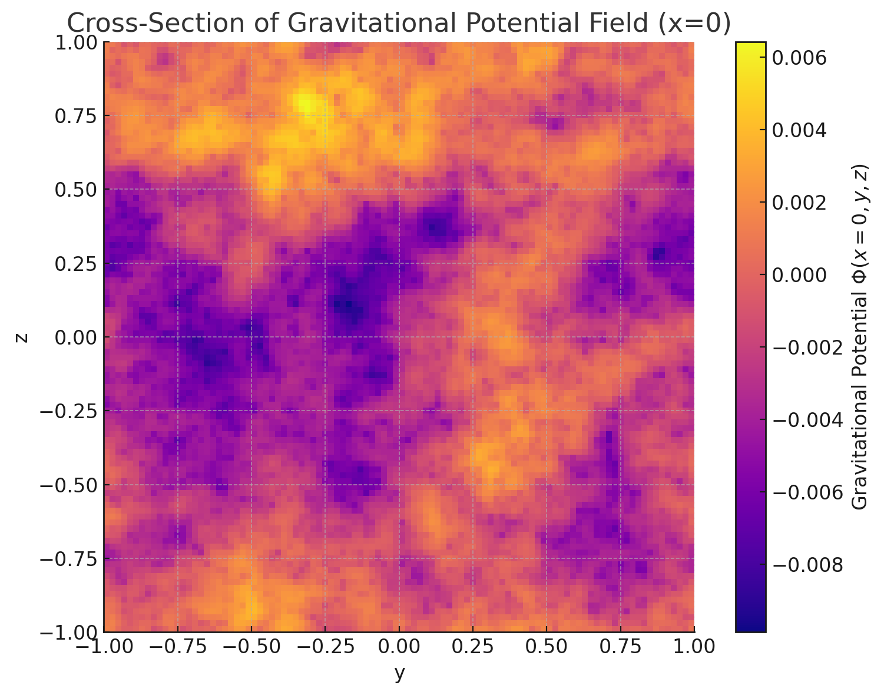
Figure 4
Title: Star Formation Potential Map (Cross-Section at x=0)
Caption:
The identified star formation potential regions, defined as areas where the gravitational potential falls below the 5th percentile. These regions represent gravitational wells deep enough to allow for matter condensation and star formation.
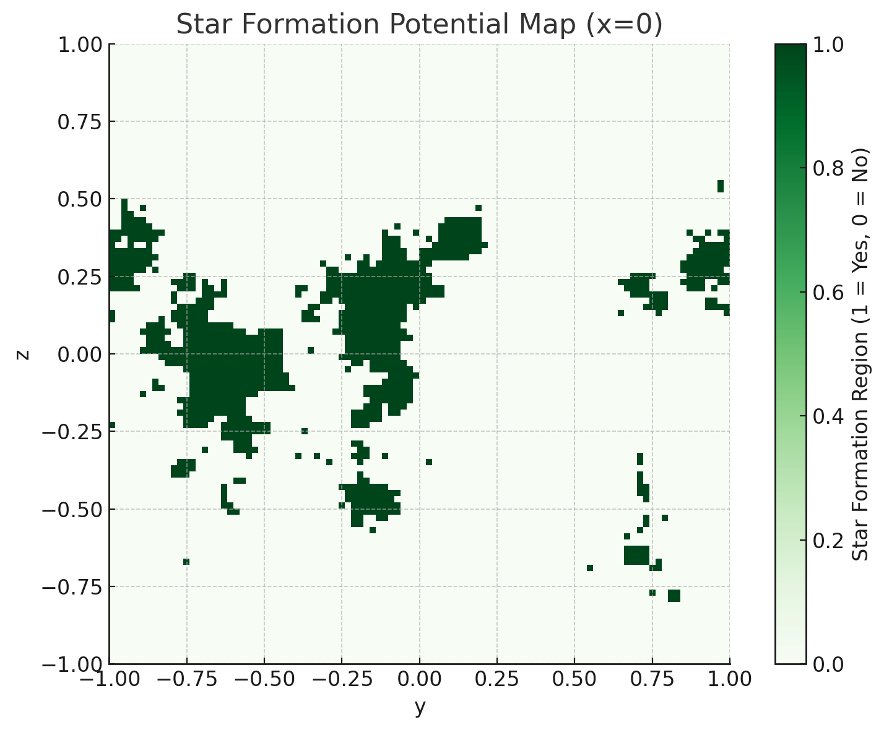
Figure 5
Title: Time Evolution Snapshots of the Information Skew Field
Caption:
Snapshots of the evolution of the information skew field at different time steps (0, 20, 40, 60, 80, 100). The field exhibits diffusion and localized contraction, leading to the development of clearer hierarchical structures over time.
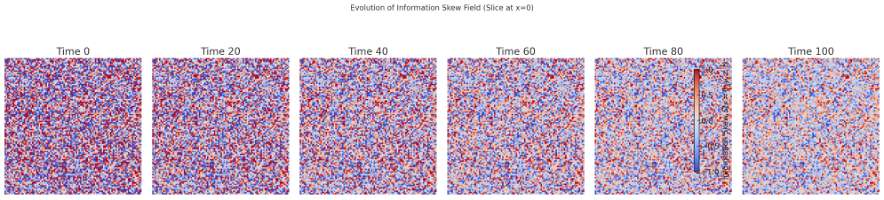
Figure 6
Title: Cross-Section of the Consciousness Emergence Potential Map
Caption:
A map of the consciousness emergence potential, combining the star formation regions with areas of high information skew. The final distribution shows localized “hotspots” of concentrated information density, suggesting self-organized structures favorable to consciousness emergence.
{利用したPythonプログラム}
図0
import numpy as np
import matplotlib.pyplot as plt
# 図0:T2Kデータに基づく情報偏倚量プロット
# エネルギー(GeV)
energy = np.array([0.2, 0.4, 0.6, 0.8, 1.0, 1.2, 1.4, 1.6, 1.8, 2.0])
# ニュートリノと反ニュートリノの振動確率
P_numu_to_nue = np.array([0.0355, 0.0473, 0.0259, 0.0155, 0.0101, 0.0071, 0.0052, 0.0040, 0.0032, 0.0026])
P_antinumu_to_antinue = np.array([0.0143, 0.0305, 0.0194, 0.0125, 0.0085, 0.0061, 0.0046, 0.0036, 0.0029, 0.0024])
# 情報偏倚量 S(E)
S_total = np.abs(P_numu_to_nue – P_antinumu_to_antinue)
# プロット作成
plt.figure(figsize=(8,6))
plt.plot(energy, S_total, marker=’o’, label=’Information Skew $S(E)$’)
plt.scatter(energy[np.argmax(S_total)], np.max(S_total), color=’red’, label=f’Peak at {energy[np.argmax(S_total)]:.2f} GeV’)
plt.xlabel(‘Neutrino Energy (GeV)’)
plt.ylabel(‘Information Skew $S(E)$’)
plt.title(‘Energy Dependence of Neutrino Information Skew’)
plt.grid(True)
plt.legend()
plt.tight_layout()
# 画像を表示
plt.show()
図1
# 図1:初期情報偏倚場 S(x,y,z) の断面図
# 初期設定
grid_size = 100 # 100x100x100グリッド
sigma_0 = 1.0 # 偏倚の最大強度
np.random.seed(42) # 再現性のため乱数シード固定
# 三次元グリッド上にガウス乱数で情報偏倚場を生成
S = np.random.normal(0, sigma_0, size=(grid_size, grid_size, grid_size))
# 中央断面 (x=0) を抽出
S_slice = S[grid_size // 2, :, :]
# プロット
plt.figure(figsize=(8,6))
plt.imshow(S_slice, extent=[-1,1,-1,1], origin=’lower’, cmap=’coolwarm’)
plt.colorbar(label=’Information Skew $S(x=0,y,z)$’)
plt.title(‘Cross-Section of Initial Information Skew Field (x=0)’)
plt.xlabel(‘y’)
plt.ylabel(‘z’)
plt.tight_layout()
# 画像を表示
plt.show()
図2
# 図2:バリオン数密度場 B(x,y,z) の断面図
# バリオン数密度場の生成(情報偏倚場の正の部分のみを抽出)
B = np.clip(S, 0, None) # S > 0 の領域のみ残す
# 中央断面 (x=0) を抽出
B_slice = B[grid_size // 2, :, :]
# プロット
plt.figure(figsize=(8,6))
plt.imshow(B_slice, extent=[-1,1,-1,1], origin=’lower’, cmap=’viridis’)
plt.colorbar(label=’Baryon Density $B(x=0,y,z)$’)
plt.title(‘Cross-Section of Initial Baryon Density Field (x=0)’)
plt.xlabel(‘y’)
plt.ylabel(‘z’)
plt.tight_layout()
# 画像を表示
plt.show()
図3
from numpy.fft import fftn, ifftn, fftfreq
# 図3:重力ポテンシャル場 Φ(x,y,z) の断面図
# 重力定数 (ここでは単位系を規格化して G=1)
G = 1.0
# バリオン数密度の平均を引いて、揺らぎ成分を作成
delta_rho = B – np.mean(B)
# 3Dフーリエ変換
delta_rho_k = fftn(delta_rho)
# 波数ベクトル作成
k = fftfreq(grid_size, d=2.0/grid_size) * 2 * np.pi # -π〜πの範囲
kx, ky, kz = np.meshgrid(k, k, k, indexing=’ij’)
k_squared = kx**2 + ky**2 + kz**2
k_squared[0,0,0] = 1e-12 # k=0での0除算を防止
# フーリエ空間でポテンシャル計算
Phi_k = -4 * np.pi * G * delta_rho_k / k_squared
# 逆フーリエ変換して実空間へ
Phi = np.real(ifftn(Phi_k))
# 中央断面 (x=0) を抽出
Phi_slice = Phi[grid_size // 2, :, :]
# プロット
plt.figure(figsize=(8,6))
plt.imshow(Phi_slice, extent=[-1,1,-1,1], origin=’lower’, cmap=’plasma’)
plt.colorbar(label=’Gravitational Potential $\Phi(x=0,y,z)$’)
plt.title(‘Cross-Section of Gravitational Potential Field (x=0)’)
plt.xlabel(‘y’)
plt.ylabel(‘z’)
plt.tight_layout()
# 画像を表示
plt.show()
図4
# 図4:星形成ポテンシャルマップ(星形成可能領域マスク)
# 星形成可能領域の閾値(重力ポテンシャルの5パーセンタイル以下)
threshold = np.percentile(Phi, 5)
# 星形成可能領域マスク作成
star_formation_mask = Phi < threshold
# 中央断面 (x=0) を抽出
star_formation_slice = star_formation_mask[grid_size // 2, :, :]
# プロット
plt.figure(figsize=(8,6))
plt.imshow(star_formation_slice, extent=[-1,1,-1,1], origin=’lower’, cmap=’Greens’)
plt.colorbar(label=’Star Formation Region (1 = Yes, 0 = No)’)
plt.title(‘Star Formation Potential Map (x=0)’)
plt.xlabel(‘y’)
plt.ylabel(‘z’)
plt.tight_layout()
# 画像を表示
plt.show()
図5
from scipy.ndimage import laplace
# 図5:情報偏倚場の時間発展スナップショット
# パラメータ設定
num_steps = 100 # 総ステップ数
dt = 0.01 # タイムステップ
D = 0.1 # 拡散係数
alpha_base = 0.05 # 基本収縮係数
# 初期情報偏倚場のコピー
S_evolve = S.copy()
# 局所収縮係数フィールド(星形成領域では収縮を強める)
alpha_field = alpha_base * (1 + 4 * star_formation_mask.astype(float))
# スナップショット保存用リスト
snapshots = []
# 時間発展ループ
for step in range(num_steps):
laplacian_S = laplace(S_evolve)
dS_dt = D * laplacian_S – alpha_field * S_evolve
S_evolve += dS_dt * dt
# スナップショットを記録(20ステップごと+最終ステップ)
if step % 20 == 0 or step == num_steps – 1:
snapshots.append(S_evolve[grid_size // 2, :, :].copy())
# スナップショットを並べてプロット
fig, axes = plt.subplots(1, len(snapshots), figsize=(20,5))
for idx, snapshot in enumerate(snapshots):
ax = axes[idx]
im = ax.imshow(snapshot, extent=[-1,1,-1,1], origin=’lower’, cmap=’coolwarm’, vmin=-1, vmax=1)
ax.set_title(f’Time {idx*20}’)
ax.axis(‘off’)
fig.colorbar(im, ax=axes.ravel().tolist(), shrink=0.6, label=’Information Skew $S(x=0,y,z,t)$’)
plt.suptitle(‘Evolution of Information Skew Field (Slice at x=0)’, y=1.02)
plt.tight_layout()
# 画像を表示
plt.show()
図6
# 図6:意識発生ポテンシャルマップ
# 正の情報偏倚のみを抽出
S_positive = np.clip(S, 0, None)
# 星形成可能領域と掛け合わせて、意識発生ポテンシャルを定義
consciousness_potential = S_positive * star_formation_mask
# 中央断面 (x=0) を抽出
consciousness_slice = consciousness_potential[grid_size // 2, :, :]
# プロット
plt.figure(figsize=(8,6))
plt.imshow(consciousness_slice, extent=[-1,1,-1,1], origin=’lower’, cmap=’inferno’)
plt.colorbar(label=’Consciousness Emergence Potential’)
plt.title(‘Cross-Section of Consciousness Emergence Potential (x=0)’)
plt.xlabel(‘y’)
plt.ylabel(‘z’)
plt.tight_layout()
# 画像を表示
plt.show()
参考文献
【1】
K. Abe et al. (T2K Collaboration),
“Constraint on the matter–antimatter symmetry-violating phase in neutrino oscillations,”
Nature, 580, 339–344 (2020).
doi:10.1038/s41586-020-2177-0
【2】
A.D. Sakharov,
“Violation of CP invariance, C asymmetry, and baryon asymmetry of the universe,”
JETP Letters, 5, 24–27 (1967).
(原論文:ソ連物理学界のバリオン非対称理論基礎)
【3】
W. Buchmuller, R.D. Peccei, and T. Yanagida,
“Leptogenesis as the origin of matter,”
Annual Review of Nuclear and Particle Science, 55, 311–355 (2005).
doi:10.1146/annurev.nucl.55.090704.151558
【4】
Planck Collaboration,
“Planck 2018 results. VI. Cosmological parameters,”
Astronomy & Astrophysics, 641, A6 (2020).
doi:10.1051/0004-6361/201833910
【5】
S. Betts et al.,
“Development of a Relic Neutrino Detection Experiment at PTOLEMY: Princeton Tritium Observatory for Light, Early-Universe, Massive-Neutrino Yield,”
arXiv:1307.4738 [astro-ph.IM] (2013).
(宇宙初期ニュートリノ観測計画の技術文書)
【6】
G. Tononi,
“An information integration theory of consciousness,”
BMC Neuroscience, 5, 42 (2004).
doi:10.1186/1471-2202-5-42
【7】
M. Tegmark,
“Consciousness as a State of Matter,”
Chaos, Solitons & Fractals, 76, 238–270 (2015).
doi:10.1016/j.chaos.2015.03.014
(初出はarXiv:1401.1219)


